 |
|  |
Nieuwe inzichten in de 2e helft van de 20e
eeuw.
In de tweede helft van de 20e eeuw zien we een ontwikkeling naar grotere
onderlinge economische en politieke afhankelijkheid (globalisering) in de wereldsamenleving.
Door de nieuwe communicatiesystemen zijn alle uithoeken van de aarde onderling
verbonden. Dat heeft natuurlijk ook gevolgen voor ons wereldbeeld, zeker nu alle
wereldgodsdiensten nauwer met elkaar in contact komen.
Ook in de kennis van
de ons omringende natuur en in de techniek vonden nieuwe ontwikkelingen plaats,
waarvan er een aantal nog niet erg algemeen opgemerkte ontwikkelingen een grote
invloed op zowel de techniek als ons wereldbeeld zullen uitoefenen. De eerste
is het systeemdenken en het gedrag van systemen ver buiten statisch evenwicht
[8]. De tweede is inzicht in de niet-lineaire dynamica ("Chaos" theorie
[9]). Helaas zijn deze ontwikkelingen niet eenvoudig, dus moeten we ze hier aan
de hand van eenvoudige voorbeelden aannemelijk maken. Voor wie verder geinformeerd
wil worden zijn er de boeken, waamaar in de tekst verwezen zal worden. In ieder
geval brengen de nieuwe begrippen ons iets dichter bij meer inzicht in het wonderbaarlijke
leven, zonder overigens de kern van het leven te onthullen. Zal dat ooit lukken? III-1.
Systeemtheorie. (zie ook Systeemtheorie
(Wikipedia))
De grote successen in de klassieke wetenschap kwamen oorspronkelijk
door de tactiek om verschijnselen of objecten van hun omgeving te isoleren en
ze dan diepgaand te bestuderen (de Cartesiaanse methode, genoemd naar Descartes).
Dat leidde tot grote ontwikkelingen in onze kennis van de natuur en van het leven.
Deze tactiek is echter niet goed bruikbaar bij de geleidelijke ontwikkeling van
machines naar systemen. Systemen berusten op de samenwerking van meerdere componenten,
zoals bij computers en netwerken, communicatie systemen, verkeerssystemen, productiesystemen
in een breed gamma van industrieen, medische systemen, enz. Hierbij is de onderlinge
wisselwerking van de componenten, die samen het systeem vormen, van primair belang.
Men kan niet meer alleen in termen van objecten (Cartesiaans) denken. Men moet
ook contextueel leren denken, door vanuit de beoogde functie van het systeem de
eigenschappen en de onderlinge wisselwerking van de bouwblokken en/of hun componenten
te specificeren. Het geheel is daardoor meer dan de som van de samenstellende
bouwblokken met hun componenten. Bij de start van de ontwikkeling van een systeem
begint men niet met het definir;ren van de componenten ervan. Men moet eerst een
redelijke zekerheid hebben over de haalbaarheid van de beoogde functie (feasibility
studie). Daarna wordt de globale opbouw van een dergelijk systeem op het niveau
van bouwblokken en hun benodigde functionaliteit bij de onderlinge wisselwerking
met de andere bouwblokken vastgelegd (globaal ontwerp).
Als voorbeeld tonen
we in fig. 5 de bouwblokken van een MRI scanner, herkenbaar in het linker schema:
een supergeleidende magneet voor opwekking van het hoofdmagneetveld, spoelen voor
een variabel hulpmagneetveld (gradient spoelen), de voeding voor die spoelen (de
gradient versterker), een hoogfrequente versterker (RF Amplifier) met de bijbehorende
zend en ontvangst spoelen, de patienttafel en een computer voor de sturing van
het systeem en de software voor de interpretatie en het archiveren van de
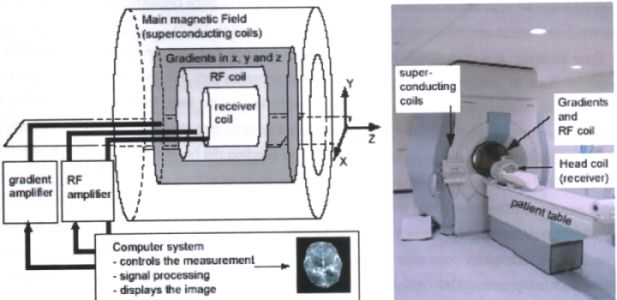
Fig. 5. Systeem voor medische diagnostiek: MRI scanner. meetgegevens.
Nadat het globale ontwerp is vastgelegd kunnen individuele bouwblokken worden
ontworpen (gedetailleerd ontwerp). Die bouwblokken zijn op zichzelf weer systemen
opgebouwd uit componenten en vaak subsystemen. Uiteindelijk bereiken we het niveau
van de specificatie van de componenten. Pas daarna kan worden begonnen met de
praktische opbouw van een systeem (engineering fase) en het testen ervan.
Voor het beschrijven van levende systemen (zie later) geldt dezelfde filosofie:
een studie van de verschillende organen apart, hoe belangrijk ook) levert een
beperkt inzicht in het geheel op. Een bloem als levend geheet leert men niet echt
kennen door de blaadjes eraf te trekken en die te bestuderen. Verder zijn de organen
op zichzelf al weer "systemen", opgebouwd uit cellen, die op hun beurt
vele chemische processen huisvesten en die in deze studie voorlopig als een "laagste"
niveau van componenten van het leven zullen worden beschouwd [10]. AI de samenstellende
delen moeten in hun context worden bestudeerd, zoals bij technische systemen,
maar die studie is veel gecompliceerder en roept steeds weer nieuwe vragen op.
Als illustratie van het bovenstaande zullen we nu een eenvoudig voorbeeld van
een systeem, n.l. een fiets en de berijder, bespreken. We beginnen met de fiets.
Stel dat die is gedemonteerd tot op de kleinste onderdelen. AI die onderdelen
kunnen apart worden onderzocht op b.v. afmetingen, materiaal, hardheid, slijtvastheid.
Als de eigenschappen van de onderdelen (componenten) bekend zijn, zal iemand die
nog nooit een fiets heeft gezien en dus het geheel aan relaties tussen de onderdelen
(de structuur) niet kent, niet op het idee komen om er een fiets van te maken.
De fiets is meer dan de som van de onderdelen. Die onderdelen kunnen ook voor
een totaal andere toepassing worden ingezet. In de hongerwinter van 1945 gebruikten
we een gedeelte van een fiets om met behulp van dynamo's licht bij elkaar te trappen,
zodat we s'avonds toch nog bij enig licht konden studeren.
Deze algemene opmerkingen
gelden natuurlijk evengoed voor andere en ingewikkeldere systemen, waarin atlerlei
verschillende onderdelen (en subsystemen) samenwerken, b.v. voor grote petrochemische
installaties en hun (momenteel meestal digitale) besturingssystemen, voor automatische
prod uctiesystemen, transportsystemen en voor wereldwijde computernetwerken. Om
al deze ontwikkelingen in kaart te brengen ontstond rond de tweede wereldoorlog
de systeemtheorie (Shannon, 1948). Maar zelfs een gemonteerde fiets, zonder
berijder kan nog niet aan zijn bestemming voldoen, n.l. de fietser van "A"
naar "B" brengen. Samen met de berijder vormt de fiets een min of meer
gesloten systeem, dat wel bepaalde relaties heeft met de omgeving (stroefheid
van de weg, tegenwind, de voeding van de berijder, de ademhaling van de berijder).
De fietser moet energie aan de rijdende fiets toevoegen, anders valt hij om. De
berijder levert die energie op basis van de voeding die hij vooraf tot zich heeft
genomen. Die energie wordt "gebruikt" om de wrijving en tegenwind te
overwinnen en het systeem wordt daarom dissipatief genoemd (dissipatie is het
verbruiken van energie, dat is: in een minder bruikbare vorm brengen, hier b.v.
warmte). Waarom blijft de rijdende fiets overeind? Omdat de fietser een afwijking
uit de verticale stand naar rechts corrigeert door een beetje naar rechts te sturen,
waardoor fietser en fiets weer in de verticale stand terugkomen. Dat heet tegenkoppeling:
de afwijking van verticaal wordt tegengewerkt. De fiets en zijn berijder blijven
verticaal door steeds, bijna ongemerkt, corrigerend bij te sturen. Ze zijn clan
in een dynamisch evenwicht, ver van de toestand van statisch evenwicht bij snelheid
nul (waarbij geen energie wordt toegevoegd en berijder op de grond moet steunen
om niet om te vallen). Wij doen dat corrigeren onbewust, maar zouden we bij een
afwijking van de verticaal naar rechts naar links sturen, clan wordt de
Fig. 6. Op zoek naar dynamisch evenwicht.
afwijking juist groter en ontstaat
er bij ver naar links sturen de kans dat de fiets en zijn berijder op catastrofale
wijze naar een statisch evenwicht terugkeren (omvallen). In dit geval spreken
we van meekoppeling: de afwijking van de verticale situatie wordt nu juist groter.
Deze inzichten in het besproken voorbeeld zijn veel algemener en zijn op veel
gecompliceerdere wijze ook van toepassing op grotere systemen, waarin veel elektronische,
mechanische of chemische componenten samenwerken, zoals dat bij grote industriele
en publieke systemen het geval is en bij levende "systemen" (b.v. het
lichaam). In de systeemtheorie wordt het geheel van het systeem onderzocht inclusief
de onderlinge relaties van de bouwblokken waarin de componenten worden toegepast.
We sommen nog even 5 fundamentele systeemeigenschappen op:
1. Er moet
energie of materie door het systeem worden geleid, er is dus wisselwerking met
de buitenwereld (open systeem).
2. Die energie wordt gedeeltelijk gedissipeerd
(in een toestand gebracht waarin we er weinig mee kunnen doen), in het geval van
de fietser door wrijvingswarmte en slijtage in de onderdelen, tegenwind, enz.
(Dissipatieve systemen).
3. De systemen zijn ver buiten statisch evenwicht
in een dynamische evenwichtstoestand.
4. Besturingsmechanismen zijn mee -
en tegenkoppeling.
5. De onderdelen moeten vervangen worden na slijtage. Levende
systemen (de fietser) vernieuwen zichzelf. Dit is op zichzelf weer een groot wonder.
Dit contextuele denken over het voorbeeldsysteem (fiets en berijder) en de genoemde
grotere systemen, is ook van toepassing op zowel veel grotere, als op veel kleinere
schaal. Men kan b.v. proberen de aarde als 6en geheel te beschouwen met het zonlicht
als externe energiebron (Gaya theorie). Een dergelijke holistische (allesomvattende)
beschouwing is natuurlijk uitermate ingewikkeld door het samen
Fig. 7.
Een klein deel van de voedingsprocessen binnen de biologische cel als illustratie
van een biologisch systeem, waarbij uit suiker energierijke stoffen worden geproduceerd,
die de functie van de cel mogelijk maken. 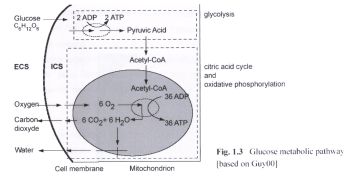
werken van een immens aantal processen, waarvan er velen nog onbekend zijn, maar
met wat al bekend is kan een eerste poging gewaagd worden. Anderzijds kan ook
een biologische cel, met zijn vele interne chemische interacties en zijn wisselwerking
met het omringende milieu (zie Fig. 7), als een systeem worden beschouwd [8].
Naast de karakterisering: "dissipatieve" systemen gebruikt men ook de
aanduiding "open" systemen, omdat energie en/of materie uitwisseling
met de omgeving kenmerkend zijn.
Maar ook individuele mensen en groeperingen
van mensen en/of organisaties (politieke partijen, geloofsgenootschappen, economische
firma's) zijn in een dergelijk beeld van systemen ver buiten evenwicht in te passen.
Er is energie nodig (menselijke activiteit, kapitaal); die energie wordt gedissipeerd
(gebruikt om de organisatie te laten functioneren), er is wisselwerking met de
buitenwereld afhankelijk van het doe/ van de organisatie, en mee en/of tegenkoppeling
moeten worden toegepast om in dynamisch evenwicht te blijven. Er zijn dus besturingsmechanismen
nodig en de deelnemers en bestuurders worden regelmatig vervangen. Ook deze organisaties
zijn hopelijk niet in statisch evenwicht.
De consequenties van het ver buiten
statisch evenwicht zijn komen in het volgende deel aan de orde. Die zijn zeer
verrassend, want ondanks het feit dat vaak de fundamentele wetten, die het systeem
beschrijven, bekend zijn en het systeem als deterministisch kan worden beschouwd,
zijn de uitkomsten vaak zeer onverwacht. Een nieuwe onzekerheid?
III-2.
Instabiliteiten, Chaos en Ordening in Open Systemen.
De eigenschappen van
open systemen ver buiten evenwicht zijn pas in de tweede helft van de 20e eeuw
boven water gekomen. Laten we eerst een eenvoudig voorbeeld beschrijven: in een
platte doos (een B6nard cel) zit een vloeistof. Warmt men de bodem op (er wordt
dus energie toegevoerd), dan ontstaat bij geringe warmtetoevoer een temperatuursverschil
over de doos, waardoor thermische geleiding door de vloeistof ontstaat. Bij hogere
warmtetoevoer ontstaat zogenaamde vrije convectie (stroming) van de vloeistof,
in het midden stijgt verwarmde (tichtere) vloeistof op, geeft de warmte af aan
het deksel om kouder

Fig. 8. Bénard cel.
(en dus zwaarder) weer fangs de buitenkant omlaag
te gaan. Een vrij homogene situatie. Convectie resulteert in een effectievere
warmteoverdracht dan bij geleiding en verlaagt dus het temperatuurverschil tussen
boden en deksel (het systeem verzet zich tegen de opbouw van een temperatuur gradi6nt
over de vloeistof). Bij een bepaalde kritische waarde van de warmtetoevoer breekt
ineens het convectiepatroon in de vloeistof op in aaneensluitende zeshoekige gebiedjes
(veel kleiner dan de doos) waar de warme vloeistof in het centrum opstijgt en
fangs de zeshoekige begrenzing weer omlaag gaat, zie fig. 8. Er is een samenhangend
(coherent) systeem van meerdere gelijkvormige zeshoekige gebiedjes (zoals een
honingraat) ontstaan. Dit is een voorbeetd van ordening in een vloeistof van aanvankelijk
onafhankelijk van elkaar bewegende watermoleculen. Hierbij is de warmteoverdracht
door de vloeistof beter, en wordt het ontstaan van een temperatuursverschil effectiever
tegengewerkt. Dit leert ons dat een systeem ver buiten evenwicht (en waarbinnen
dus energie moet worden gedissipeerd) plotseling in een andere geordende toestand
kan overspringen. Welke "dirigenY' bestuurt de geordende (coherente) beweging
van miljarden in eerste instantie onafhankelijke watermoleculen?
Als de warmtetoevoer
door de bodem van de Benard cel nog groter wordt kan de vloeistof zelfs weer in
een ongeordende toestand (chaos, turbulentie) overspringen. Daarbij is het warmtetransport
nog effectiever. We hebben dus een overgang van geleiding naar convectie gezien,
vervolgens rangschikte de convectiebeweging zich in een soort honingraat en bij
weer meer warmtetoevoer ontstond turbulentie (chaos). Verderop zullen we zien,
dat mathematische modellen van open systemen ook dergelijke plotselinge toestandsovergangen
vertonen.
Er zijn in de natuur veel voorbeelden van overgangen van orde naar
chaos en vise versa. Een bekend voorbeeld is het optreden van turbulentie in stroming
(zoals het opbreken van de waterstraal uit de kraan). Ook het inschakelverschijnsel
van lasers, die bij een bepaalde kritische waarde van de toegevoerde energie in
plaats van niet gebundeld (incoherent) licht plotseling zeer nauw gebundeld (coherent)
licht gaat uitzenden is een voorbeeld van zo'n overgang. Gelukkig maar, want die
coherente lichtbundel maakt het uitlezen van de kleine putjes in een CD mogelijk,
zodat we van onvervormde muziek kunnen genieten. Ook geleiden glasvezel kabels
coherent laserlicht over grote afstanden, waardoor breedband communicatie mogelijk
wordt.
Een ander bekend voorbeeld is het hart. Na vele jaren van actief in
een toestand van dynamisch evenwicht het bloed regelmatig door het lichaam te
stuwen, kan het plotselinge ritme stoornissen gaan vertonen of zelfs gaan fibrilleren.
Dan is er dus een verandering van een geordende toestand van dynamisch evenwicht
naar een chaotische toestand. Als het fibrilleren de hartkamers betreft zijn de
gevolgen vaak zeer ernstig en soms fataal en een oorzaak is moeilijk aanwijsbaar.
Met een pacemaker en/of een defibrillator kunnen de gevolgen vaak worden bestreden,
zodat erger wordt voorkomen.
V6br het computertijdperk kon de wiskunde het
optreden en de dynamica van de plotselinge overgangen in open systemen in het
algemeen niet beschrijven in verband met het niet-lineaire karakter van de beschrijvende
mathematische maiellen. Slechts een beperkte klasse van natuurverschijnselen kon
kwantitatief worden bestudeerd, en hoewel er een indrukwekkend aantal van zulke
wiskundige oplossingen zijn gedocumenteerd, moest men zich beperken tot kleine
afwijkingen van een bekende toestand. Daarmee kan soms de inzet van instabiliteiten
worden aangegeven, maar de volledige gang van zaken bij de instabiliteit onttrekt
zich aan onze berekeningen. Met open systemen ver buiten statisch evenwicht en
hun plotselinge toestandsveranderingen was er dus nauwelijks ervaring. En juist
deze open, dissipatieve systemen komen overvloedig in de natuur, zowel de "dode"
als de "levende", voor en bieden via hun toestandsveranderingen een
mogelijkheid van toenemende ordening in de evolutie [9], [6]. Is hier sprake van
een scheppingsprincipe?
Een voorbeeld uit de chemie is de spontane vorming
van katalytische cycli, bestudeerd door Eigen c.s. in de jaren zestig, zie [8].
Zij vonden dat bij katalytische reacties in biochemische systemen ver buiten evenwicht,
dus afhankelijk van toevoer van energie, er zich gecompliceerde netwerken vormen
waarin mee- en tegenkoppeling als sturingsmechanismen voorkomen. In zo'n netwerk,
vaak een gesloten structuur waarin het laatste enzym het eerste weer ontmoet,
fungeert het ene enzym als katalysator voor het volgende enzym in het netwerk
van reacties, waardoor terugkoppeling mogelijk wordt. Dit lijkt op een prebiologisch
stadium in de evolutie!
We kunnen ons nu afvragen: hoe het mogelijk is dat
er overgangen zijn van een toestand van chaos naar een toestand van ordening.
Eerder hebben we gezien dat in gesloten systemen de entropie (de mate van wanorde)
altijd toeneemt tot maximale wanorde is bereikt. Voor een open systeem als zodanig
hoeft deze wet echter niet te gelden; die geldt namelijk voor het totale systeem,
dus voor het open systeem plus de omgeving waarmee de energie of materie uitwisseling
plaatsvindt. Dat totale systeem is dan weer een gesloten systeem. Als dus de wanorde
in de omgeving, waarmee uitwisseling plaats vindt, voldoende sterk toeneemt, kan
de entropie van het beschouwde open systeem afnemen, dus de interne orde (en dus
de opbouw en de organisatie) ervan toenemen.
Dat opent de mogelijkheid tot
het ontstaan van nieuwe geordende structuren (met lagere entropie (11]). Dat betekent
schepping van nieuwe ordening uit een bestaande minder geordende situatie.. De
natuur kent vele voorbeelden. Levende systemen zijn altijd open systemen en zijn
dus afhankelijk van dit principe voor het evolueren en het voortbestaan van hun
geordende structuren [8]. Is niet het zoeken van voedsel (als inkomende materie
en/of energiestroom) en het verwijderen van afval voor elk levend wezen een eerste
levensnoodzaak? III-3. "CHAOS" Theorie, Niet Lineaire Dynamica.
(Zie ook Chaostheorie (Wikipedia))
De analytische wiskunde, die halfweg de vorige eeuw beschikbaar was, had
zich enerzijds ontwikkeld uit het werk van de Griekse filosofen die de antwoorden
voor hun problemen vaak zochten in geometrische modellen. Anderzijds was de bijdrage
van de Islamitische filosofen uit Persi(~, die (via de Arabieren) de algebra introduceerden
in de westerse cultuur, een bron van inspiratie. Descartes bracht beide methoden
op meesterlijke manier samen en werd daarmee de grondlegger van de moderne analytische
wiskunde, die in de 18e en 19e eeuw tot grote bloei kwam. Bij het kwantitatief
beschrijven van actuele verschijnselen in de natuur moest men zich echter noodgedwongen
voornamelijk beperken tot situaties waarvoor het mathematische model met analytische
methoden oplosbaar was of oplosbaar gemaakt werd door het geldigheidsgebied te
beperken tot geringe afwijkingen van een bekende evenwichttoestand. Daarbij worden
de vergelijkingen "gellneariseerd", d.w.z. alle variabelen komen slechts
in de eerste macht voor. Daarmee kan, zoals gezegd, hoogstens het begin van een
instabiliteit worden aangetoond, maar de boven beschreven ptotselinge toestandsveranderingen
in open systemen zijn allesbehalve gering en dus moeten de oorspronkelijke niet-lineaire
vergelijkingen worden bestudeerd en die zijn slechts in enkele gevallen analytisch
oplosbaar. Er ontstond dus behoefte aan een nieuwe methode om de niet-tineaire
vergelijkingen op te lossen. De ontwikkeling van de computer maakte de weg vrij.
In de 60er jaren van de vorige eeuw had Lorenz, een weerkundige van het Massachusetts
Institute of Technology in Boston, een stelsel vergelijkingen opgeschreven voor
de luchtdruk, de temperatuur en de windsnelheid, waarmee hij het weer in de komende
weken meende te kunnen voorspellen. Omdat die vergelijkingen te gecompliceerd
waren om ze met de bekende analytische methoden op te lossen werden ze in een
grote computer geprogrammeerd en werden er z.g. numerieke optossingen gegenereerd.
Lorenz ontdekte dat de numerieke oplossingen van zijn vergelijkingen zeer kritisch
afhangen van de begincondities: zeer kleine wijzigingen in de begintoestand kunnen
uiteindelijk totaal andere oplossingen tot gevolg hebben. Lorenz uitte zijn verwondering
hierover met de vraag: "Kan het fladderen van een vlinder in Brazilie een
orkaan doen losbarsten in Texas"? De begincondities voor het weersysteem
kan men slechts met beperkte nauwkeurigheid op een beperkt aantal plaatsen op
aarde en in de atmosfeer door metingen te weten komen, dus het weer is maar beperkt
voorspelbaar, zoals we in ons deel van de wereld maar al te goed weten [9].
Lorenz' studie markeerde het begin van de "Chaos" theorie, [9]
[12], nu aangeduid als niet-lineaire dynamica. Het is een zeer gecompliceerde
mathematische ontwikkeling en ik mag hopen dat ik het voor mezelf en de lezer
enigszins aanvoelbaar kan maken. Eeuwenlang heeft de analytische wiskunde veel
bijgedragen tot het kwantitatief beschrijven van natuurkundige verschijnselen.
Het toepassen van de wetten van Newton en de thermodynamica en ook de "moderne"
kwantummechanica en relativiteitstheorie zijn daar overtuigende voorbeelden van.
De berekeningen waren echter vaak, zoals gezegd, beperkt tot kleine afwijkingen
van bekende situaties (lineaire - of gelineariseerde verge lijkingen). Maar zelfs
een eenvoudige wrijvingsloze slinger kan alleen bij kleine uitwijkingen worden
beschreven door een lineaire (differentiaal)vergelijking, bij grote uitwijking
is de vergelijking niet meer lineair. De komst van de computer halfweg de vorige
eeuw maakte het oplossen van vergelijkingen ver buiten het toen bekende ("lineaire")
gebied mogelijk en confronteerde de onderzoeker met geheel nieuwe en onverwachte
resultaten voor open systemen ver buiten statisch evenwicht.
III-3-1.
Begincondities.
Die grote afhankelijkheid van de begincondities die Lorenz
ontdekte blijkt ook op te treden in veel eenvoudiger situaties, zoals de beweging
van een dubbele slinger. Hierbij is aan het uiteinde van een enkelvoudige slinger
een tweede slinger opgehangen. We nemen aan dat beide slingers wrijvingsloos zijn.
We kunnen nu de beide slingers een bepaalde uitwijking geven (begintoestand) en
uitrekenen hoe deze slingers als functie van de tijd bewegen. Dat uitrekenen gebeurt
op basis van de wetten van Newton. Daarna starten we een tweede experiment met
een begintoestand die een fractie afwijkt van die bij het eerdere experiment.
De dan uitgerekende beweging lijkt dan nog een korte tijd op de beweging van het
eerste experiment, maar na enige tijd ontstaat een toenemende afwijking ervan
en spoedig lijken de bewegingen in de twee experimenten in het totaal niet meer
op elkaar; het lijkt wel chaotisch. Een mooie demonstratie van de beweging van
een dubbele slinger is te zien op Internet (zie onder http://www.science.uva.nl/misc/pythagoras/interactief/java/penduluml).
Dat betekent dus een nieuwe onzekerheid in onze mogelijkheden om de natuur kwantitatief
te beschrijven en te voorspellen. Hoewel het systeem deterministisch is moeten
de begincondities vaak beter bekend zijn dan onze meetinstrumenten toelaten. Bij
kwantummechanische situaties kunnen we ten gevolge van de onbepaaldheidrelaties
van Heisenberg (Zie II-2) de begintoestand zelfs principieel niet nauwkeurig kennen,
laat staan de latere ontwikkeling van een systeem voorspellen! Dat geldt des te
meer voor de evolutie van het heelal, van het leven en van het menselijke gedrag,
waarbij we de begincondities alleen maar kunnen gissen. MN:
Een Zoektocht naar God.
| | |
 LITURGIE
&CETERA
LITURGIE
&CETERA  LITURGIE
&CETERA
LITURGIE
&CETERA